One of my funniest friends is known nowadays as Lord Christophe π
Lord Christophe deserves a beautiful original brainteaser in his honour, and so here it comes…! ππ
Lord Christophe finds a perfectly flat, horizontal, rectangular, gorgeous green garden. Its mathematical properties are so delightful that he decides to buy it!
It has length L metres, width (unbelievably π) U metres, perimeter P metres, and area A square metres.
P, A, U and L are all whole numbers.
Lord Christophe also loves the fact that, for his special garden, P = A.
He laughs out loud when he learns that LORD CHRISTOPHE rearranges to make SPORT CHILD HERO πππ€£
So, he picks the speediest mathematical student of Musica Mundi School to sprint in a perfect straight line diagonally across the garden from one corner to the diagonally opposite corner, then diagonally back again.All that is to be done ten times…
…and like The Flash or a rocket!
And now, dear friends, this is your Prize Brainteaser: The total distance (in metres) that the student sprints equals the square root of C, where C is a whole number. In honour of Lord Christophe, what is the exact maximum possible value of C ?
Please feel free to send me your best answers by email ππ
A lot of the loveliest photos around the school are by Lord Christophe. I think that the following recent photo was by him; it’s certainly a gorgeous one to enjoy π
Please also have fun with the following wonderful Chess puzzle from a recent training game of mine. It’s Black to play and win π
It’s Black to play and win π
A Facebook friend of mine named Antonio posts beautiful, inspirational daily messages to spread the truly Good News of The Bible for as many people as possible to benefit from knowing it.
We’re already 50 days into 2024, but I have been so busy trying to do my best with many commitments that I’m only now finally finding time to publish my first blog post of this year. As I met up with lots of Chess friends in recent days during the school holiday, it’s a pleasure to now share many happy moments via nice photos πβ€οΈπ
I saw this stunning image β€οΈ on the Facebook page of Grandmaster Alexander Baburin, an old Chess friend of mineA lovely photo β€οΈ of Grandmaster Koen Leenhouts holding his prize and his son, Max, at the closing ceremony of a recent great Chess tournament in Wachtebeke, BelgiumI was highly impressed in Wachtebeke by the play of numerous talented and very strong young players, some of whom are pictured above ππOn the left is Jacob Dreelinck, a young Chess super-talent, and in the middle is Yordi De Block who performed very well indeed, too, and was also undefeated in Wachtebeke ππOlder generation players (including myself!!) also had a fabulous time in Wachtebeke β€οΈ
Time for a quick, wee Chess joke…!!
What’s the first name of a brilliant Belgian Chess player who can be as good as a Woman International Master!?
Answer: Wim!
P.S. If you see me with a black/blue bruise soon, you’ll know my joke backfired!! π
Johan Krijgelmans works enthusiastically on Chess, and I reckon that he’s going to keep getting better and better ππValΓ¨re De Buck and I fought a good Chess battle in the final round of the Senior Tournament in Wachtebeke ππ. I was of course delighted to win the event with a score of 6/6, and I wish to thank organiser Dennis van Vliet and his entire team for doing everything so well. It was also a pleasure to play and get to know Luc, Wim, Johan, Pierre, Thierry and ValΓ¨re.The runner-up who won second prize with 4.5/6 in the Senior Tournament in Wachtebeke was Pierre Theon ππ, a super-experienced (now retired) Mathematics teacher from France.
To do well in Mathematics or Chess it’s essential to practise a lot, and that requires precious time and great dedication.
I will now share with you an original Maths brainteaser which I created to celebrate the birthday of a friend named Eric who was turning 66 earlier this month…
I sent this on 9 February:
“Suppose that the Quadratic EquationΒ x2Β + bx + c = 0
has two positive whole number solutions for x.
In honour of Eric’s birthday on 12 February, we’ll say that c – b = 122.
Your Prize Puzzle Challenge now is to solve the equation x2 + bx + c = 0.
Please feel free to send me your two solutions for x by 12 February ππ
Wishing you lots of fun and happy solving,
Paul/Mr. Mπ.”
Eric used EXCEL to solve the puzzle, which was OK as it was for his birthday, after all!! π
In general, though, I always hope that some people will send in a beautiful analytical solution worked out by themselves.
Warm congratulations to 14-year-old Wonderful Wout Callens who did solve the puzzle and sent me this, for which I will be delighted to present him with a nice prize in school this week:
“Dear Mr. Mo,
These are the steps I used to solve the problem:
c-b = 122 so c = b+122.
As the solutions are required to be positive whole numbers, we can derive from the quadratic formula that b<0 and that β(b2 – 4ac) must be a whole number.
We know that a=1 and that c=b+122 and substituting that into the square root and rearranging the expression, we get that β((b-2)2 -492) must be a whole number.
Then I tried out values for b for which β((b-2)2 -492) was equal to a whole number and found the values b=-42 or 46, but as b<0, b =-42.
Hence c=122-42=80.
Substituting a=1, b=-42 and c=80 into the quadratic equation, we get that x equals either 2 or 40.
Enjoy your holidays π
Wout.”
Thank you and congratulations again, dear Wout! ππ
I wrote personally to Eric on his birthday to say,
Dear Eric,
Happy birthday!! Have a really wonderful time!
CongratulationsΒ on finding that x = 2 or 40 in the puzzle I sent on Friday.
In this New Year ’24, add up 24 + 2 + 40 to get a nice total for your birthday!!!
With kindest wishes as always to your whole family,
Paul π.
Now, keen young or older fans of Mathematics could be interested to learn that there actually exists a super-fast method for solving the puzzle in a matter of seconds without even needing a calculator, and without even needing to figure out the individual values of b or c!! First, I will present a quick piece of theory which helps to crack the puzzle speedilyπ
Suppose that the solutions to the quadratic equation x2Β + bx + c = 0 are x = p or x = q. Then (x-p)(x-q) = 0, which leads us to x2-(p+q)x + pq = 0. Comparing coefficients in the quadratic equations can help us to realise that p+q = -b and pq=c. (Note: Those results can also be proved using the Quadratic Formula.) So, c-b = pq+p+q. Next comes a highly noteworthy mathematical trick… c-b+1 = pq+p+q+1 which factorises to (p+1)(q+1).
In the specific case we had where c-b = 122, we get that c – b + 1 = 123, and so (p+1)(q+1) = 123 = 3 x 41 (or 1 x 123). Therefore, since the puzzle required that p & q had to be positive whole numbers, it follows that p+1 = 3 & q+1 = 41 (or vice-versa), and p=2 & q=40 (or vice-versa). π
Those positive solutions are unique, but having a different value for c-b such as 2 would mean that c-b+1 = 3 which is 1 x 3 for (p+1)(q+1), and then we wouldn’t be able to get positive solutions for both p & q. Also, a different value for c-b such as 23 would mean that c-b+1 = 24 which is (1 x 24 or) 2 x 12 or 3 x 8 or 4 x 6 for (p+1)(q+1), and we would consequently get several possible pairs of values for p & q (unless we were to pin down specific individual values for b & c rather than just saying what value c-b has).
Quick Word Puzzle:
Rearrange the letters of RETRIED to make another proper seven-letter word also beginning with R.
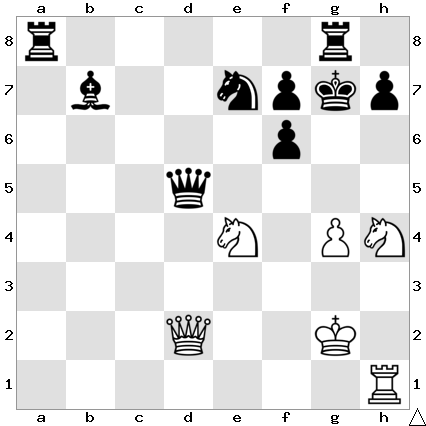
Valère De Buck was rightly very pleased to discover a beautiful finish as White (to play and win) in a lovely game of his in Wachtebeke.
ValΓ¨re calculated 1 fxe4 fxe4 2 Qg4+ and then 2…Kf6 3 Rf1+ or 2…Qf5 3 Rxe4+ Kf6 4 Rf7+ or 2…Kxd6 3 Bf4+! gxf4 4 Qxg6+ or 3…Kc6 4 Rc7#, checkmate! β€οΈ
Solution to Word Puzzle (given earlier, above):
RETIRED
I will round off this article with the following message:
The time is coming ever-nearer when everyone will know the answer to the question “Who can we count on totally to fulfill every important promise?” No matter what obstacles anyone might seem to cause (either deliberately or unintentionally), we can rest assured that the Will of God always prevails exactly when God wills it, and the timing is always perfect, no matter whether we think it is or not! One key theme permeating the Book of Numbers within The Bible is God’s unwavering fulfillment of promises, and that still holds true, no less now than ever. A very positive, warm reminder of blessings is this: “The Lord bless you and keep you; the Lord make His face shine on you and be gracious to you; the Lord turn His face toward you and give you peace.”–Numbers 6:24-26. π
The Bible verse wording is very slightly different in the image above, but the good message always remains essentially the same π
I do most sincerely wish everyone a really blessed Christmas, and I now offer a nice selection of fresh, home-made puzzles for free consumption and enjoyment!! ππ
A Merry Christmas Surprise! π
Start with the total number of letters in MERRY CHRISTMAS EVERYBODY. Multiply by the total number of letters in PROMISES. Also multiply by the total number of letters in FULFILLMENT. Did the final result bring a nice smile to your face!? π
Early Happy New Year Brainteaser! π
Suppose that ‘a’ and ‘b’ are whole numbers such that 1 < a < b < 2023.
What is the minimum-possible value of the fraction b/asuch that 2023 * b/a equals some future year?
Puzzle Fans Brainteaser!! βοΈπ
Seasonal Celebrations at Musica Mundi School, Waterloo, Belgium πΆπ
Suppose that whole numbers 1, 2, …, N are about to be given out randomly to N people (one number each), so that each person’s number will be different. Two people will multiply their own numbers together. All the other people will multiply their own numbers together. The latter group is certain that their result will be the bigger product. To guarantee that, what is the minimum value of N?
Three Sneaky Word Puzzles πππ
Remove only the letter E from A HEART BRO and then rearrange the remaining 8 letters to make the name of a lovely coastal town which is the largest town in the county of Angus in the East of Scotland. (That will be a nice ‘n easy puzzle for Scott Fleming, a friend who lives there!! π)
Think of a beautiful musical instrument which has 5 letters when written in plural form with s on the right end. Move only the s to the start to make a different proper 5-letter English word.
ππΆ
Also, rearrange the letters of LYRICS END to make the proper name of a mathematical shape (in plural form, with s on the right end).
Deep-Thinking Brainteaser! ππ
The image (which is NOT drawn to scale!) is a front-view sketch of a cylindrical pipe of diameter d, partially filled with water to a depth h = d/5 (at the deepest part throughout the pipe). The pipe is only P% full (that is, P% of its maximum capacity). The brainteaser challenge is to figure out the value of P, correct to 4 significant figures βοΈπ
Quick ‘n early New Year Bπnus
Suppose that Y is the value of 100*P, correct to 4 significant figures. In the New Year 2024, we’ll be able to say that it’s then X years since the start of the year Y. What is the value of X? (You don’t have to count the small change of ten days made to the Gregorian calendar in 1582 !!)
A Magical Family Brainteaser! ππ
Suppose that I know a lady whose birthday is on the same day and month as that of her daughter. The daughter’s age (in years) is now D, which is a whole cube number. The talented mathematical daughter said to her mum, “Your age now, multiplied by my future age after any number of years, would be exactly the same as my age now, multiplied by your age twice as far into the future!”
Based on the information above, what was the most probable age of the mother when her daughter was born? Justify your answer with a reason.
A Number Mystery Brainteaser! βοΈπ
In honour of Scottish friend Scott Fleming, I am thinking of a personal special three-digit whole number ABC. It’s exactly equal to E * EG, where EG represents not E*G but rather the unique two-digit whole number EG which has the same value as G2+E. Your fun brainteaser is to figure out exactly what number ABC is!
Extra Bπnus!
What is special about the value of E2+G2+H2+I2 where HI represents the first two digits of the number Y which featured in an earlier bπnus in this blog post?
This position is from a recent training game in which I was Black against a strong Chess engine. It’s Black to move, and your fun puzzle is to figure out the forced checkmate in 10 moves that I played in the actual game π
It’s my intention to publish solutions to all the puzzles around the time that blog post #163 comes out, God-willing as always. (Before then, I will finally publish solutions to the puzzles of blog post #161 !)
Please do feel free to send me your best solutions to any or all of the puzzles, if you like π.
I would like to round off this article by most sincerely wishing you again a very blessed Christmas and New Year soon, with lots of happiness in everything that you do β€.
With kindest wishes as always,
Paul Mπtwani β€
“It is the Lord who directs your life, for each step you take is ordained by God to bring you closer to your destiny.”–Proverbs 20:24 π
My thanks to the Murphy Family for the lovely gift of cosy socks that they very kindly gave me yesterday. My steps will surely be all the warmer from now on!! π
The concept of ‘Parity’ is even more important in relation to people than it is with regard to whole numbers in Mathematics. Two numbers are of equal parity (no matter how big or small they are) if they are either both even or are both odd numbers, but all people are loved infinitely by God, our Creator, and so no-one is less important than anyone else. In that respect, we have parity (equal importance). Each person is unique, though, and I would like to very sincerely wish you lots of happiness and success in using your personal gifts to do as much good as you can. π
A photo from the Chess Club at Musica Mundi School π
Puzzle: We awarded 1 point for a win, 0 for a loss, 0.5 to each player in the case of a draw. Five players are (at least) partly visible in the photo. Their total points awarded from the games pictured turned out to be 3 points.
What conclusion can you deduce from that information? πβοΈ
Wonderful Quotation: “To listen to the Word of God, listen with your ears and hear with your heart”–Pope Francis π
Word Puzzle: Rearrange the letters of PRAY IT to make a proper, six-letter English word.
Bonus Word Puzzle: Rearrange the letters of PREP HOW to make a seven-letter word.
Extra Bonus Word Puzzle!!: Rearrange the letters of FED MORE to make a seven-letter word. ππ
With Chess Friends Jelle, Hans, Lennert and Remy π
Two people I know well, who both have birthdays tomorrow, are Ask-Johannes (a Norwegian teenager) and Michael-Roy (the eldest son of Paul & Gill, very dear Scottish friends of mine). π
A Nice Numbers Happy Birthday Brainteaser for Tomorrow, 22 November, in Honour of Ask-Johannes and Michael-Roy ππππ
The new ages tomorrow of Ask-Johannes and Michael-Roy will be numbers of the same parity (meaning both even or both odd, as mentioned earlier), and Ask-Johannes will still be a teenager. The product of the two new ages will be almost 222.
Part 1: What precisely are the two new ages if I tell you that their product is the largest number it could be that fits with the clues?
Part 2: How exactly do you know that the product cannot be 1 more than in Part 1? There might seem to be a solution which works with the larger product, but why doesn’t it?
Part 3: To determine the correct new ages in Part 1, why was it important to know that they are numbers of equal parity?
Part 4.1: Ask-Johannes’ older teenage sister, Vilja, had her birthday last week. Tomorrow, Ask-Johannes’ new age A will be of equal parity to Vilja’s age V. How old is Princess Vilja?
Part 4.2: What is most special about the day coming in A+V days from now?
Part 5: Scott Fleming from Arbroath, Scotland, is one of my friends on Facebook. I would like to offer early, advance, happy birthday wishes to Scott. A wee bonus puzzle for everyone else is to figure out Scott’s birthday (just the day and month) if I tell you that it’s in A days from now.
A Happy Birthday Brainteaser for Today, 21 November, in Honour of Murad, Marie, Ian and Chris, all friends of mine on Facebook!!!! ππππ
The sum of the four friends’ new ages is 212, a palindrome.
Murad is the youngest, but finished being a teenager several years ago. He is now M years old.
The sum of Marie’s and Ian’s new ages is M+100.
Chris’s new age is the biggest of the four, and it’s a palindrome.
How old is Murad?
Quick, Wee Bonus Part π
A few days ago, I played in a Chess match in a very pleasant location at Hundelgemsesteenweg number 10*M in Merelbeke, Belgium. π
I won with Black in 10*M – 200 moves.
Everyone in the two teams was offered really nice complimentary refreshments during and after the Chess match.
Here are a few photos from the day.
After the game with Joris ππ
With Eric Van de Wynkele, owner of the lovely pieces of art ππ
It’s my intention to publish solutions to all the puzzles around the time that blog post #162 comes out, God-willing as always. (Before then, I will finally publish solutions to the puzzles of blog post #160 !) By the way, without needing to calculate the results, which of the numbers 158, 161 or 162 equals the product of two numbers of the same parity (given that one of the three choices is correct)!?
Please do feel free to send me your best solutions to any or all of the puzzles, if you like π.
I would like to round off this article by most sincerely wishing you a very blessed month of December soon, with lots of happiness in everything that you do β€.
With kindest wishes as always,
Paul Mπtwani β€
“The Lord always forgives everything! Everything! But if you want to be forgiven, you must set out on the path of doing good. This is the gift!”–Pope Francis.
P.S. = Puzzle Solutions (being posted now on 27 December 2023)
The boy standing up must have won his Chess game. Reason: The total number of points for each game is 1 (either 1 point to the winner or 0.5 to each player in the case of a draw). So, the total for the two games involving four seated players was 2 points, but we were told that the grand total–including the boy visibly standing–was 3 points. Therefore, he scored 1 point, which means that he must have won his game. π
PRAY ITβPARITY
PREP HOWβWHOPPER
FED MOREβFREEDOM π
Ask-Johannes = 16 & Michael Roy = 30.β16 x 30 = 480, just four less than 484 = 222.
Note that 483 = 3 x 7 x 23, which doesn’t involve any teenage option.
The same is true of 482 = 2 x 241.
481 = 13 x 37 might seem to work, but we were basically told that Ask-Johannes was already a teenager, and so he wouldn’t just be turning 13 this year.
Also, being told that Ask-Johannes and Michael-Roy have ages of equal parity enabled us to be sure that the solution was 16 x 30 = 480 rather than 480 = 15 x 32 (which would involve numbers of different parity). π
Princess Vilja = 18 (older than Ask-Johannes, but still a teenager whose age is of the same parity). π
A+V = 16 + 18 = 34, and 34 days after the first publication date of this blog post was…Christmas Day!! β€οΈ
Scott Fleming’s birthday was on 7 December. π
Murad = 23 (Marie + Ianβ123; Chris = 66; the grand total = 23 + 123 + 66 = 212). π
161 = 7 x 23, the product of two (odd) numbers of the same parity.
Note that neither 158 nor 162 are multiples of 4, and so neither of them could be the product of two even numbers. βοΈ
In the previous blog post, I featured ‘The Saints’ Little Book of Wisdom’, which is such a precious gem of a book that I am very warmly recommending it again here, to everyone. There are so many good things to learn by reflecting on and practising in our lives the pearls of wisdom contained in the book.
In addition to the quotes within the lovely image above, another favourite of mine from St. Teresa of Avila is: “You pay God a compliment by asking great things of Him.” π
As usual, I also have several good-fun puzzles to share ππ
A Kettle Puzzle! π
My kettle at home displays 100 when the water in it boils. Afterwards, as the water cools gradually, the display number drops by 1 unit (degree Celsius) at a time, until it finally settles at around room temperature.
Looking at the photo above, I said to myself, “The temperature has dropped by 72Β° (from 100Β°) down to 28Β°. 72 x 28 = 2016.”
Kettle Puzzle Part 1
If I were to observe the temperature all the way while it dropped from 100Β°, and at each moment calculate
Temperature drop from 100 x Temperature displayed
what would be the maximum result that I could get like that? βοΈπ
Kettle Puzzle Part 2
The example result of 2016 (given above) ends with a 6. What is the probability that I could get a result ending in my favourite 3? π
(Please assume that I do my calculations correctly!!)
Cheers to Chess Puzzle!
Instead of drinking hot chocolate as in the photo above, I often drink delicious Musica Mundi School apple juice while I’m enjoying Chess with the students.
Suppose that 46 students drink a collective total of 350 cups of apple juice, and they all drink at least one cup each.
Cheers to Chess Puzzle, Part 1
As a very reasonable mental Maths exercise (without using any calculator), figure out, correct to 1 decimal place, the Mean (Average) number of cups of apple juice drunk per student.
Try to write a sentence or two to describe clearly the method you used to figure out your answer mentally. π
Cheers to Chess Puzzle, Part 2–A Brainteaser!! π
Given the information stated before Part 1, what is the maximum possible value for the Median number of cups drunk?
Cheers to Chess Puzzle, Part 3
If the maximum possible Median actually occurs, then what is the Modal number of cups drunk?
Also, what is then the Range = Maximum – Minimum number of cups drunk?
Welcome to Misato, Puzzle!
Misato, our newest wonderful student at Musica Mundi School, came all the way from Australia to Belgium this week. Helen, one of the English teachers, told me that Misato is really strong in her subject. So, I made now a nice word puzzle in honour of Misato.
Word Puzzle for Misato, Part 1
Remove just the letter A from MISATO, and then rearrange the remaining 5 letters to make a proper 5-letter English word. Try to find two different, correct solutions. βοΈπ
Word Puzzle for Misato, Part 2
Remove just the letter I from MISATO, and then rearrange the remaining 5 letters to make a proper 5-letter English word. Again, try to find two different, correct solutions. π
A Cute Double Checkmate Chess Puzzle!!
If it’s Black to move, checkmate can be forced in 5 moves.
If it’s White to move, checkmate can be forced in 4 moves.
Have fun solving that cute double checkmate Chess puzzle!! π
It’s my intention to publish solutions to all the puzzles around the time that blog post #161 comes out, God-willing as always. (Before then, I will finally publish solutions to the puzzles of blog post #159 !) By the way, without needing to calculate the result, which of the numbers 159, 160 or 161 equals the sum of the first eleven prime numbers (given that one of them is correct)!?
Please do feel free to send me your best solutions to any or all of the puzzles, if you like π.
I would like to round off this article by most sincerely wishing you a very blessed month of November soon, with lots of happiness in everything that you do β€.
With kindest wishes as always,
Paul Mπtwani β€
“In all created things, discern the providence and wisdom of God, and in all things give Him thanks”–St. Teresa of Avila.
P.S. = Puzzle Solutions (being posted now on 30 November 2023)
Kettle Puzzle Part 1: Maximum-possible result = 50 x 50 =2500.
Kettle Puzzle Part 2: None of the results in this particular Maths “story” can ever end with a digit 3, and so the probability of such a result occurring is simply zero. (Basically, it was a “trick question”!! π)
Cheers to Chess Puzzle, Part 1: To calculate 350 Γ· 46 mentally, one method is as follows…
7 x 46 = 7 x (50 – 4) = 350 – 28 = 322, with 28 still “to spare” from the 350 cups in the puzzle.
Next, 28 Γ· 46
= (23 + 5) Γ· 46
= (46/2) Γ· 46 + (4.6 + 0.4) Γ· 46
= 1/2 + 1/10 + nearly 1/100
= 0.5 + 0.1 + less than 0.01.
Putting that together with the chunky 7 found earlier…
the correct quotient result for 350 Γ· 46 will be…
7.6 for the Mean, correct to 1 decimal place βοΈ
Cheers to Chess Puzzle, Part 2: Imagine the 46 students lined up in order, starting with the students who drank the least number of cups, and then going all the way up to the students who drank the most. The Median will be found in the middle of the long line by calculating
(the total number of cups drunk by Student #23 & Student #24) Γ· 2.
To maximise that result, let the first 22 students drink only 1 cup each (not zero, though, because we were told that everyone drank at least one cup each). Then, we have retained 328 cups to share amongst the final 24 students.
328 Γ· 24 = 13.7 (approx.), and so the most that we can allocate to Student #23 is 13 cups (whole number).
Then 315 cups still left Γ· 23 students = 13.7 cups per student (approx.), and so the most that we can allocate to Student #24 is again 13 cups (to also have a whole number of cups for him or her).
Therefore, the maximum-possible Median = (13 +13) Γ· 2 = 13 cups. π
Cheers to Chess Puzzle, Part 3: Following on directly from everything written in Part 2 above, imagine that we just give Students #25 up to #46 only 13 cups each. We’ll have “used up” 22 x 1 + 24 x 13 = 334 cups with just 16 cups still “to spare” from the total of 350.
At that moment, 22 students have 1 cup each & 24 students have 13 cups each (and we’ll get to the spare 16 in a wee moment!). As things stand right now, the mode is 13. It’s the “winner”!
Can any other number overtake it in popularity, by using the “spare” 16 cups…?
Well, if (for example) we bumped up 16 of the numbers 13 each to 14, then we’d have this situation: 22 students with 1 cup each, 8 students with 13 cups each, and 16 students with 14 cups each. The mode in that case would be 1.
To illustrate a couple of other alternatives…we could have 6 students with 1 cup each, 16 students with 2 cups each, and 24 students with 13 cups each. The mode in that case would be 13.
We might alternatively have 22 students with 1 cup each, 22 students with 13 cups each, and 2 students with a “lucky 21” cups each! The joint winners there for popularity are 1 and 13: they are both modes in this case, and in summary they are the only possible modes when the maximum median of 13 occurs. π
Word Puzzle for Misato, Part 1
MISATO – A = MOIST or OMITS.
Word Puzzle for Misato, Part 2
MISATO – I = ATOMS or MOATS or STOMA. π
A Cute Double Checkmate Chess Puzzle!!
If it’s Black to move, checkmate can be forced in 5 moves with 1…Rg1+! 2 Rxg1 Rxg1+ 3 Kxg1 Qg4+ 4 Kh1 (longer than 4 Rg2 Qxg2#) 4…Qd1+ 5 Rf1 Qxf1#.
If it’s White to move, checkmate can be forced in 4 moves with 1 Qa8+ Kd7 2 Qb7+ Kd8 3 Qb8+ Kd7 4 Qc7#. π
Regarding the sum of the first eleven prime numbers, 2+3+5+7+11+13+17+19+23+29+31=160. Even without calculating the actual result, we could know that it had to be even, because ten odd numbers make 5 pairs of odd numbers, equivalent to a sum of 5 even numbers. That has to be even, and adding on 2 (the smallest prime, and the only even prime) keeps the total even for sure. π
I try to be grateful always for every moment that God grants, and this summer was filled with wonderful people, places, events and countless other blessings.
On holiday in Croatia; sunset in Zadar β₯Our first evening, in Dubrovnik β₯
Just one of the special companions for me during three open international Chess tournaments–one in Germany and two in Belgium–was The Saints’ Little Book of Wisdom (compiled by Andrea Kirk Assaf).
One of my absolute favourite quotations from this gem of a book is: “Every moment comes to us pregnant with a command from God, only to pass on and plunge into eternity, there to remain forever what we have made of it.”–St. Francis de Sales β₯1st= on 6 out of 7 (5 wins & 2 draws) at the Senior International Open Chess Championship in Magdeburg, Germany β₯ Everywhere I went this summer, I was delighted to make many new friends, and meet up with great old friends too.The Belgian Senior International Open Chess Championship, Round 2 on 7.8.2023 β₯Belgian Senior International Open Chess Championship Prizegiving 1st= on 4.5 out of 5 π2nd= on 7.5 out of 9 (6 wins & 3 draws) at the Belgian International Open Rapid Speed Chess Championship. I’m pictured there with International Arbiter, Geert Bailleul πPaul & Jenny pictured at Krk Island, Croatia β₯Paul & Jenny during a nice walk in Zagreb, Croatia β₯Paul & Jenny at a lovely restaurant during the final evening in Zagreb β₯Beautiful Night at the Atomium β₯
Creative Puzzles Time!! βππ
Puzzle #1, Part 1
Write down the proper English name for the mathematical 3D shape shown above. Then rearrange the letters of the name to make another proper English word π
Puzzle #1, Part 2
Suppose that, in the diagram above, the dimensions r, h and L are all whole numbers of centimetres.
Part 2.1: Explain how you can then be absolutely sure that r, h and L must all be different, distinct numbers.
Part 2.2: Also, what is then the absolute minimum possible value for
the sum r + h + L?
Part 2.3 Brainteaser:
Thinking ahead with hope to blog post #160 (God-willing as always), can you discover suitable whole number values for r, h and L such that r + h + L = 160?
Puzzle #2
Think back to Blog Post #158…Can you discover a fitting reason for why June 7 was the perfect date for that post to be published?
Puzzle #3(Brainteaser)
Suppose that Beethoven is writing down the same one-digit whole numbers that friends Jens, David, Jan, Herman, Peter and Paul are thinking of. Among us six seated friends, it turns out that we are all thinking of the same number…except for Paul! So, five of our numbers are identical; only Paul’s number is different. When Beethoven multiplies the six numbers together correctly, he gets a particular year that was just the second year of a certain century in the past. Exactly what year does Beethoven get in this puzzle!? π
Very warm congratulations to my niece in England on achieving fabulous top results in all of her national exams this summer π Hearty congratulations also to every one of my Musica Mundi School students who sat Cambridge Mathematics exams this year, as they all succeeded really well ππ
Suppose that my niece in England and her dad play almost 100 Chess games together. To encourage really good, combative play, I award three points for a win, 1 point each for a draw, no points for a loss. After all the games have been played and points have been duly awarded according to the results, we calculate
Total Points of the Two Players Γ· Number of Chess Games they Played.
In their case, that turns out to be a decimal number a.b, in which ‘a’ is the whole number part, and ‘b’ is the one-digit decimal part.
If we convert the decimal number a.b to a fraction in its simplest form, we get c/d, where c and d are prime numbers, and a, b, c and d are all different.
Given the information above, your Sunset Girl Mega-Brainteaser in honour of my niece is to figure out the exact maximum-possible number of games of Chess that she played with her dad. Also, exactly how many of those games ended with a decisive win/loss result, and exactly how many of the games ended as draws?
Puzzle #5: Checkmate! π
It’s White to play & win by force in a real Grandmaster clash from 1962, the year when I was born π
It’s my intention to publish solutions to all the puzzles around the time that blog post #160 comes out, God-willing as always. (Before then, I will finally publish solutions to the puzzles of blog post #158 !)
In the meantime, please do feel free to send me your best solutions to any or all of the puzzles, if you like π.
I would like to round off this article by most sincerely wishing you a very blessed month of September soon, with lots of happiness in everything that you do β€.
With kindest wishes as always,
Paul Mπtwani β€
“As gifts increase in you, let your humility grow, for you must consider that everything is given to you on loan, from God”–St. Pio of Pietrelcina.
“The secret of happiness is to live moment by moment and to thank God for all that He, in His goodness, sends to us day after day”–St. Gianna Beretta Molla.
P.S. = Puzzle Solutions (being published now on 30 October 2023)
CONEβONCE.
Pythagorasβ Theorem tells us that L2=r2+h2.
There are, of course, cases in which itβs possible for r and h to equal each other,
but then L2 = 2r2
and so L = β2*r.
Thatβs not possible if L, r and h have to all be whole numbers (because β2, the square root of 2, is an irrational number).
Therefore, if L, r and h are positive whole-number dimensions on the cone, they must all be different from each other, and the slant height L must be greater than r and also greater than h.
In that case, the minimum-possible value for r+h+L is 3+4+5 = 12.
The consecutive whole numbers 3, 4, 5 form the most famous Pythagorean Triple: 32+42=52.
Whole numbers fitting the challenge r+h+L=160 are 32, 60 & 68. Note that 322+602=682. Also, the numbers 32, 60, 68 are four times larger than the famous 8, 15, 17 Pythagorean Triple in which 8+15+17=40.
June 7 was the perfect day for Blog Post #158 to be published because it was the 158th day of 2023.
Beethoven would get 1701 (the second year of the 18th century) by correctly calculating 3 x 3 x 3 x 3 x 3 x 7.
In the brainteaser about Chess games, a.b = 2.6 = 13/5 = c/d.
a=2, b=6, c=13, d=5 with c and d being prime, as was stated in the puzzle.
60% of all the games end decisively and 40% of all the games are draws, which is why a.b = 2.6 or 3 β 0.4. (If all the games had ended decisively, then a.b would have reached its maximum-possible value of 3.)
The maximum-possible number of games (less than 100) is n=95, of which 60%β57 games are decisive wins and 40%β38 games are draws. Note: We wouldnβt get whole numbers there if n wasnβt a multiple of 5.
In the puzzle about Chess moves from 1962, White can win with 1 Qe6! Qxe6 2 Rxh7#, a neat checkmate! πππ
The birthdays coming on weekdays next week include my birthday in n days from now and my wife’s birthday in 3n/2 days’ time π. In the meantime, though, Jenny and I would like to wish both a very happy birthday tomorrow to our dear friend WGM (Woman Chess Grandmaster) Erika Sziva, and a continued strong recovery from her recent operation in hospital.
β₯ A Perfect Peaceful Picture of Poppies by WGM Erika Sziva β₯
We would also like to wish a really happy birthday later on in 2n = 2*n days from now to Richard, one of the lovely new friends whom we met recently at a super party in Luxembourg πππ
Richard was delighted to receive one of the n+2 prizes that were in my bag!! π
Puzzle #1
As 3 is my absolute favourite number, this first fun warm-up puzzle is a triple or three-part puzzle πππ…It’s to figure out the dates this month of Jenny’s birthday, Richard’s birthday, and the number of prizes that were in my bag πΉ
Michael, Jenny & me pictured on 31 May with three of our friends π, the tallest of whom is Jerry, a star student in Singapore π
Puzzle #2: Double Brainteaser for Jerry & all Maths fans! π
A rectangle (that is not a square) has a perimeter of P units (e.g. P cm) and an area of A square units (e.g. A cm2).
Part 1: It can be proved that, for all such rectangles, P2 > J*A, where J is a particular, special whole number. Enjoy figuring out, with proof, the maximum value for J that still makes the inequality P2 > J*A true for all such rectangles.
Part 2 of the brainteaser is to figure out (with proof) an expression in terms of P and A for the radius of the largest circle which can fit inside the rectangle. π
πΆ There is a noteworthy spiritual analogy…God makes His Holy Spirit available to guide and help us at all times. When we stay ‘tuned in’ and properly connected within, all is well. In our lives now, we should remember and respect where the boundaries are.
The diagram shows a large square (with a dark-coloured outline) containing four congruent rectangles and another square, which all fit in exactly.
Part 1: If the area of the large square is A square units, find (with proof) an expression in terms of A for the perimeter of one of the inner rectangles.
Part 2: Suppose that the perimeter of the inner square is not less than the perimeter of one of the four congruent rectangles. Determine (with proof) the minimum possible value of the ratio longer side : shorter side for any of the four congruent rectangles. β
Puzzle #4: A Power of Love Brainteaser ππ
Since God is perfect Love, Love really ought to have 1st place in our lives. So, L=1 in this brainteaser. I discovered that if LOVE is a four-digit whole number–and therefore OV is a two-digit whole number–then there is just one, unique solution to the equation
LOVE = OV * EE (with L=1).
Your lovely brainteaser is to figure out (with proof) the value of the number represented here by LOVE. π
Puzzle #5: A Loving Sequel Starring Coco the Cute Cat!! π±βπ
When solving Puzzle #4, Cute Coco, a super-mathematical cat, found the correct value for LOVE.
Now in Puzzle #5, and here in Blog Post #158, it’s fitting that
158 * C + D = LOVE,
where D is the day-number in June of my birthday, and C is a nice, positive number in honour of clever Coco π±βπ
Your fun puzzle is to figure out the values of C and D. ππ
P.S. I hope you’ll enjoy all the puzzles every bit as much as Coco’s owner, Mr. Jan Vanderwegen, who is Musica Mundi School’s excellent I.T. Manager ππ
Puzzle #6: A Word Puzzle in Honour of Coco π
Can you think of a plural, 11-letter, proper English word starting with the letters coco which refers to two (or more) people who create something together? πΆ
Puzzle #7: Black to play & force checkmate in 8 moves π
This position is from a recent training game Computer vs Paul π I was delighted to discover the correct way for Black to force checkmate in 8 moves π Enjoy figuring it out now, too! π
For all chess-related items, I can warmly recommend http://www.debestezet.nl, a top-quality site π run by WGM Erika Sziva and her husband, Robert Klomp. Erika & Robert also have http://www.raindroptime.com π
It’s my intention to publish solutions to all the puzzles around the time that blog post #159 comes out, God-willing as always.
In the meantime, please do feel free to send me your best solutions to any or all of the puzzles, if you like π.
I would like to round off this article by most sincerely wishing you a very blessed month of June, with lots of happiness in everything that you do β€.
Also, I would like to particularly wish all students of Musica Mundi School success in their class concerts next week, and in all the other exciting events still to come in the remainder of the current school year πΆπ. For the graduating students, I am sure that their research presentations and musical performances will be wonderful and extremely interesting π. One of the students who is about to graduate is Antigone, and it’s also her birthday this week. Happy birthday, and have a really wonderful time, Antigone! ππ
With kindest wishes as always,
Paul Mπtwani β€
“My Father is glorified and honored by this, when you bear much fruit, and prove yourselves to be My true disciples.”–Bible verse, John 15:8 π
P.S. = Puzzle Solutions (being posted–at last!–now on Tuesday 29 August 2023)
Puzzle #1: n=6; Jenny’s birthday was 16 June; Richard’s birthday was 19 June; there were 6+2=8 prizes in my bag π
Puzzle #2: Part 1
If the rectangleβs Length, Width & Area are represented by L, W & A respectively, then
L*W=A
so W = A/L.
Also, the Perimeter, P=2L+2W
βP=2L+2(A/L)
β2L2-PL+2A=0, which can be thought of as a Quadratic Equation in L.
The standard textbook condition for it to have two distinct, real solutions for L (corresponding to the cases L Λ W or, alternatively, L < W)
is that its Discriminant b2-4ac Λ 0.
In this case, that means (-P)2-4*2*2A Λ 0
which simplifies to give P2 Λ 16A.
The puzzle stated that P2 Λ J*A.
So, now we have discovered that J = 16, the maximum value for J that would be guaranteed to hold true for every rectangle that is not square. Note that, specifically for all squares, P2 = 16A exactly, and so itβs actually pretty logical then that P2 Λ 16A for non-square rectangles. π
Puzzle #2: Part 2
Now imagine fitting a circle of radius r inside the rectangle.
Let’s assume that L < W (though the correct final expression for rmax will not change at all even if L Λ W).
The diameter of our circle cannot exceed L, as otherwise some of the circle would be outside the rectangle.
So, the maximum value of r is such that 2r = L β rmax = L/2.
Returning now to our earlier Quadratic Equation2L2-PL+2A=0,
and using the standard Quadratic Formula given in lots of textbooks,
the smaller of the two solutions for L (corresponding to L < W ) is given by
L = (P – sqrt(P2 – 16A))/4.
Therefore, since we already deduced that rmax = L/2,
we now reach the result that rmax = (P – sqrt(P2 – 16A))/8. π
Puzzle #3:
Part 1
Let the four congruent inner rectangles each have dimensions L & W.
They then each have a perimeter of P = 2*(L+W).
Also, each side of the large square is L+W, and its area is therefore given by
A = (L+W)2
βL+W = sqrt(A)
and so
P = 2*sqrt(A). π
Part 2
Let’s assume that L < W.
Then note that each side of the inner square will be W – L.
If its perimeter is not less than the perimeter of one of the aforementioned rectangles, then
4*(W-L)β₯2*(L+W)
β4W-4L β₯ 2L+2W
β2W β₯ 6L
and so
W/L β₯ 3. π (If we had assumed W < L, we would have ended up with L/W β₯ 3.)
Puzzle #4
The unique solution to LOVE = OV * EE (with L=1) is OV=59 & E=3, so LOVE=1593=59*33 π
Restrictions on the size of OV * EE (big enough to get a four-digit result, yet not too large given that L = 1 only) helped to narrow down the options and home in quickly on the one correct solution πβ
Puzzle #5
Given 158 * C + D = LOVE = 1593 now,
it’s clear that C = 10 & D = 13 works perfectly π
Puzzle #6
COCOMPOSERS ! πππΆπΆ
Puzzle #7
The main checkmating sequence is 1…Qe2+ 2 Kg2 Nh4+ 3 Kg3 (or 3 Kg1 Qe1+ 4 Rxe1 Rxe1#) 3…Re3+!, after which White’s line of best resistance is 4 fxe3 Nf5+ 5 Kf4 Qxe3+ 6 Kxg4 (6 Kxf5 Qg5#) 6…Nh6+ 7 Kh4 Qg5+ 8 Kh3 Qg4# πβ
Special congratulations to the Van Steerteghem Family of Eric, Martine, Nick and (last, but certainly not least!!) my brilliant colleague, Jens. They tackle and solve the puzzles with great enthusiasm and success! ππ
In a future blog post, I will enjoy sharing with you some of the nice puzzles that they gave me for my birthday.
For now, though, I will simply conclude this post here with three lovely photos of my top puzzle solvers! πππ
“He will be a joy and a delight to you, and many will rejoice because of his birth.”–Bible verse, Luke 1:14 π
Given that we are children of God, created in His image, it’s lovely to get to know one another, and gently help each other to become ever more what our Creator made us to be. When we use well and share our God-given gifts for the benefit of others, there is no limit to the good that can be accomplished.
Staying ‘tuned in’ to the Holy Spirit and coming to know God’s word and His will through Bible study and prayer also helps us to understand more about ourselves and each other. When we then interact with gentle, loving patience and kindness, problems are often solved very happily with miraculous ease! ππ
Nice Word Puzzle π
Use all the letters of ARC SMILE to make a proper 8-letter English word.
There are (at least) three possible solutions!
Keep a smile on your face and a rainbow in your heart π
I recently promised a friend that this article being offered freely here would include some good, fun number/number-theory puzzles. I wish you lots of enjoyment with them now. πβ
Power of Friends Brainteaser π
The ages of five special friends are consecutive whole numbers, represented here by A, B, C, D and E. Andy is the youngest, followed by Beth, Chris, Dee and Eric, the oldest. The five friends are staying together at a large holiday house until 31 May. The house number (on the front door) is represented here by H Λ 1.
A remarkable detail is the fact that 31 x 5 x (HA + HB + HC + HD) = HE β HA.
Your super-fun brainteaser is to figure out, with proof, the exact value of the house number H. π
New 2023 Brainteaser π
The 2023 brainteaser is to figure out, with proof, all possible positive whole number values for N such that N – 1 is a factor of N2 + 2023.
Not 2023 π
Double All-Play-All Chess Brainteaser (with no Chess moves!! πβπ€£)
Suppose that P players are having a double all-play-all Chess tournament, and P Λ 2. Each player will play against each other player twice: once with White, and once with Black. In each game, if there’s a winner, he/she gets 1 point and the loser 0 points; if the game ends in a draw, then the two players involved receive 0.5 points each. At the end of the tournament, each player’s final score will be the total sum of the points that he/she received in his/her games.
Suppose that the gold medal winner in 1st place actually achieves the very highest possible score π, and the silver medal winner in 2nd place achieves what is then the highest-possible runner-up score (lower than the winner’s score, though).
It turns out that the number obtained by dividing the winner’s score by the runner-up’s score does not involve more than one distinct, different digit when you write it out.
The brainteaser is to figure out, with proof, three possible values for P, the number of players. ππ
A Double High-Five Brainteaser!! ππ
Consider all non-negative whole numbers n with not more than D digits.
The brainteaser is to figure out (as an expression, with proof) how many of them are such that n10 + 1 is exactly divisible by 10.
Suppose that ‘a’ and ‘b’ are distinct non-zero numbers such that
a2 + 2ab – 3b2 = p & 2a2 – 3ab + b2 = q.
The triple challenge is to find a neat, simplified expression for ‘a’ in terms of p, q & b AND to discover three values for p Γ· q which are NOT possible in this brainteaserAND to find a proper, mathematical, English word which contains a, b, p and q (not necessarily in that order) at least once each among its letters!!!
Chess Puzzle (with moves this time!! ππ)
It’s White to play & win πβ
It’s my intention to publish solutions to all the puzzles around the time that blog post #157 comes out, God-willing as always.
In the meantime, please do feel free to send me your best solutions to any or all of the puzzles, if you like π.
I would like to round off this article by most sincerely wishing you a very blessed month of May and a wonderful weekend now, with lots of happiness in everything that you do β€.
Beautiful Bonus! πππ
Extra-special wishes to lots of people I know who are celebrating their birthdays today! You can write down any proper three-digit whole number that you like (e.g. 523). Repeat it to get a six-digit number (e.g. 523523). Divide by 2 in honour of our friendship. Now divide by 7, the number of letters in FRIENDS. Also divide by 13, the total number of letters in HAPPY BIRTHDAY. To finish, divide by the three-digit number that you started with…
The final result of…π 5.5…is to wish you a beautiful birthday now on 5 May πππ
With kindest wishes as always,
Paul Mπtwani β€
“For shoes, put on the peace that comes from the Good News, so that you will be fully prepared.”–Bible verse, Ephesians 6:15 π
P.S. = Puzzle Solutions (being posted on 12.5.2023)
ARC SMILE rearranges to make MIRACLES (and you could claim that it makes CLAIMERS or RECLAIMS too!! π).
In the big H brainteaser, we were given that
31 x 5 x (HA + HB + HC + HD) = HE β HA
where A, B, C, D & E are consecutive whole numbers in increasing order, and so
155 x HA x (1+H+H2+H3) = HA x (H4 – 1)
and ‘cancelling’ the common factor HA on both sides of the equation gives
155 (1+H+H2+H3) = (H4 – 1)
and then factorising the expression on the right-hand side leads to
155 (1+H+H2+H3) = (H-1) (1+H+H2+H3)
which simplifies to
155 = H-1
so H = 156, which is nice here in blog post #156 π
In the ‘2023 Brainteaser’, we were given that
N – 1 is a factor of N2 + 2023, and since N2 + 2023 = (N-1)(N+1)+2024,
N-1 must also be a factor of 2024β1, 2, 4, 8, 11, 22, 23, 44, 46, 88, 92, 184, 253, 506, 1012 or 2024 for N-1,
and so
N can be any of the sixteen numbers 2, 3, 5, 9, 12, 23, 24, 45, 47, 89, 93, 185, 254, 507, 1013 or 2025.
In the Double All-Play-All Chess Tournament with P players,
the maximum-possible score (for someone who wins every single game) is 2(P-1), and in that case the maximum-possible runner-up score (for someone who wins every single game apart from the two games lost against the super champion!) is 2(P-2).
The winner’s score divided by the runner-up’s score simplifies to (P-1)/(P-2).
There are three possible values of P for which (P-1)/(P-2) produces positive results that in each case don’t require more than one distinct, different digit when written out. They are P = 3 or 11 or 12, and the corresponding (P-1)/(P-2) values are 2, 1.111… repeated and 1.1 exactly.
In the Double High-Five Brainteaser, n10 + 1 is exactly divisible by 10
βn10 + 1ends with a digit 0βn10 ends with a 9βn5 ends with a 3 or a 7βn itself ends with a 3 or a 7; that is precisely two out of each ten numbers ending with 0 to 9, because only the ones ending in 3 or 7 actually work here. Now, the total number of non-zero whole numbers with not more than D digits is 10D. So, the total number of suitable numbers for n is 10D x 2 Γ· 10,
which simplifies to 2 x 10D-1 πβ
In the advanced Advanced Algebra Triple Brainteaser, where
‘a’ and ‘b’ are distinct non-zero numbers such that
a2 + 2ab – 3b2 = p & 2a2 – 3ab + b2 = q,
factorisation leads to
(a-b)(a+3b) = p & (a-b)(2a-b) = q
so p/q = (a+3b)/(2a-b). Since a is not equal to zero, p/q is not equal to -3; since b is not equal to zero, p/q is not equal to 1/2; since a is not equal to b, p/q is not equal to 4. In summary, p/q cannot equal -3, 1/2 or 4.
Also, the equation p/q = (a+3b)/(2a-b) can be rearranged to make ‘a’ the subject. We get a = (p+3q)b/(2p-q). That equation helps to confirm again that, since a is not zero, p+3q is not zero, so p/q is not -3. Similarly, 2p-q can’t be zero, so p/q can’t equal 1/2. Also, a is not allowed to equal b in this puzzle, so (p+3q)/(2p-q) can’t equal 1βp+3q β 2p-qβ4q β pβp/q β 4.
Mathematical words containing the letters a, b, p and q include equiprobable and equiprobability.
In the Chess puzzle,
White wins beautifully with 1 Qxh6+!! Kxh6 2 Rh3+ Kg5 (2…Kg7 3 Rh7#) 3 f4+! Kxf4 (or 3…Kf5 4 g4+ Kxf4 5 Rf1+ Kg5 6 Rh7 and 7 h4#) 4 Rf1+ Kg5 5 Rh7! followed by 6 h4#! π
I’m not just 3 or 4 days early with surprises here…it’s actually 34 + 4 days in advance of the 12 July birthday of Jens Van Steerteghem, a brilliant colleague who loves solving fun brainteasers, as do many of our students at Musica Mundi School πΆπ
Just yesterday evening, a special idea which involves “Jens’ 12/7″π came to me, and so I decided happily to share this surprise π super-early now!! π It was tempting to wait until tomorrow and then be precisely 12 x 7 days before 12 July…but instead we’re (12 – 7 + 12) x (12 – 7) days early! π
OK, here we go… There’s literally an infinite choice for pairs of numbers a and b such that a2 β b2 = 12/7. Imagine that I pick such a pair, and I whisper the numbers to Eric and Martine (Jens’ lovely parents) ππ.
To turn up the sneaky-level button π, Eric then calculates a2 + 2ab – 3b2 and Martine calculates 2a2 – 3ab + b2.
Next, Nick (Jens’ brother) multiplies Eric’s and Martine’s results together.
The Advanced Algebra Birthday Brainteaser for Jens (and other great solvers!) to figure out is this: what is the most extreme final result that Nick could get?
In other words, the ‘most extreme’ possibility is either a minimum value or a maximum value. The fun challenge is to determine which of those two is correct, and also to figure out the actual extreme value.
To make the challenge all the more interesting and surprising, it can be completely solved without using Calculus at all! So, it really is an Advanced Algebra brainteaser coming far in advance of Jens’ 12/7 birthday!
Compared to that one, a very wee snack bonus puzzle, here in Blog Post #155, is to use all six of the numbers 3, 4, 3, 4, 7 & 12 to make 155. Parentheses ( ) and operations involving +, -, x, Γ· can be used freely, as you wish.
Another quick one is: how can the digits within 12 and 7 combinein a somewhat different type of calculationto get the result 127?
And here’s quite a nice puzzle: how many whole numbers from 1 to 1000 inclusive do not contain Jens’ favourite digit 7?
The following neat brainteaser gives me happy memories… π How old was I when I could then truthfully say (all in relation to that time), “The product of my age n years ago and my age n years from now is 1207”? π
Joke Time! π
With apologies to lovely lady Martine, why should men be good at solving the earlier algebra brainteaser?!
Answer: Martine Eric & Nick (MEN) were starring in it! π€£
To make up for that one…I’ve got another algebra brainteaser for Jens’ family and everyone to enjoy!
The picture shows regular shapes. The double brainteaser is to figure out the value of a + b + c + d, and also find the maximum possible value of the product a*b*c*d. πJens’ father, Eric, particularly likes ‘The Royal Game’ of Chess π In this puzzle, White is 7 points down on material (using conventional values), but can you find a beautiful way to still win? π
It’s my intention to publish solutions to all the puzzles around the time that blog post #156 comes out, God-willing as always.
In the meantime, please do feel free to send me your best solutions to any or all of the puzzles, if you like π.
I would like to round off this article now by most sincerely wishing you a very blessed week, with lots of happiness in everything that you do β€.
With kindest wishes as always,
Paul Mπtwani β€
βI am the vine; you are the branches. If you remain in me and I in you, you will bear much fruit; apart from me you can do nothing.”–Bible verse, John 15:5
P.S. = Puzzle Solutions (being posted on 12.5.2023)
Let a2 + 2ab – 3b2 = p and 2a2 – 3ab + b2 = q. Then 3p + 2q = 3(a2 + 2ab – 3b2) + 2(2a2 – 3ab + b2), which simplifies to 7a2 – 7b2 or 7(a2 – b2). We were given that a2 – b2 = 12/7, and so 7(a2 – b2) = 7*12/7, which is 12. We’ve proved that 3p + 2q must have the constant value 12. That is, 3p + 2q = 12 is absolutely forced, given that a2 – b2 = 12/7.
So, q = (12 – 3p)/2, and the product pq = p(12-3p)/2 or -1.5p2 + 6p. Using standard facts regarding quadratic expressions, the graph of the function f(p) = -1.5p2 + 6p would be a parabola with a maximum value when p = -6/(2*-1.5)βp = 2. The actual maximum value of the function is then -1.5*22 + 6*2β-6 + 12β6 is the maximum-possible value π
One may ask, how can we be sure that it’s really possible to have p = 2 and q = 3 in order to achieve pq = 6, the claimed maximum-possible value of pq when a2 – b2 = 12/7 ? Do suitable values exist for ‘a’ and for ‘b’ which would get us to p = 2 and q = 3 ? Well, if you check out the solutions to the next blog post (#156), you’ll see a proof showing that a = (p+3q)b/(2p-q). Requiring p = 2 & q = 3 also then requires that a = 11b. So, (11b)2 – b2 = 12/7β121b2 – b2 = 12/7β120b2 = 12/7βb2 = 1/70βb = 1/β(70) or -1/β(70) and, since a = 11b, we find that a = 11/β(70) or -11/β(70) πβ
Here in Blog Post #155, we were invited to use all six of the numbers 3, 4, 3, 4, 7 & 12 to make 155. Parentheses ( ) and operations involving +, -, x, Γ· could be used freely, wherever we wish. One solution is (3+3+7) x 12 – (4Γ·4) = 155. Note that it’s also perfectly sufficient to write (3+3+7) x 12 – 4Γ·4 = 155 if we’re familiar with the standard, internationally-accepted rules regarding ‘Order of Operations’ πβ
In the next puzzle, 27 – 1 = 127 π
Just as there are one thousand whole numbers from 1 up to and including 1000, there’s also one thousand such possibilities from 000 to 999. However, if we exclude numbers containing any 7, then for each of the three – – – place-value positions, we only have nine (instead of ten) options (namely 0, 1, 2, 3, 4, 5, 6, 8, 9 but not 7), and so the total number of such possibilities is 9 x 9 x 9β729 π
How old was I when I could then truthfully say (all in relation to that time), “The product of my age n years ago and my age n years from now is 1207”? Note that 1207 = 17 x 71, and the number mid-way between 17 & 71 is (17+71)/2 which is 44. Note also that 44 – 27 = 17 & 44 + 27 =71. So, I was 44 when I could truthfully say, “The product of my age 27 years ago and my age 27 years from now is 1207.” π
The picture shows regular shapes. The double brainteaser is to figure out the value of a + b + c + d, and also find the maximum possible value of the product a*b*c*d. π
We use the facts that each interior angle of a regular hexagon, regular pentagon and a square is 120Β°, 108Β°, 90Β° respectively. We also make repeated use of the fact that the sum of the angles in a triangle is 180Β°. So, the angles immediately to the left and to the right of the top vertex of the pentagon are (60-a)Β° and (60-b)Β° respectively, with a 108Β° angle between them. Therefore, (60-a)Β° + (60-b)Β° + 108Β° = 180Β°βa + b = 48.
Similarly, the angles just above the top edge of the square are (18+c)Β° & (18+d)Β°. So, (18+c)Β° + (18+d)Β° + 108Β° = 180Β°βc + d = 36.
Therefore, a + b + c + d = 48 + 36 β84.
Also, the maximum-possible value for the product a*b*c*d is 24*24*18*18β186624 π
White wins beautifully with 1 Qh6+!! Kxh6 2 Nf5++ Kg6 3 Rh6#or via the similar 1…Kh8 2 Ng6+ & 3 Qxh7#or 2 Qxh7+ Kxh7 3 Nf5+ Kg6 4 Rh6# π
Here in Blog Post #154, with the coming (in just a few days’ time) of Easter–which celebrates Jesus Christ’s triumph over death, and the gift of eternal life to faithful followers–a perfect Bible verse to recognise properly with gratitude and joy is: “Then, when our dying bodies have been transformed into bodies that will never die, this Scripture will be fulfilled: Death is swallowed up by triumphant Life.”–1 Corinthians 15:54 β₯
The above truly is infinitely more important than anything at all relating to Chess or Mathematics, for example, but still I’m now going to happily share a feast of nice, fresh puzzles ππ
FUN BRAINTEASER π
A girl makes a lovely cuboid-shaped gift box for her father for Easter. The total outer surface area of the closed box is 386 cm2. Its dimensions (length, width and height) in centimetres are each different positive whole numbers, which are also the ages (in years) of the girl and her two younger siblings.
Your fun brainteaser is to figure out all of their ages. The puzzle can be solved using neat algebra πβ
A 2023 PUZZLE π
If S is the smallest positive whole number for which the sum of the digits equals 2023, then what is the sum of the digits of S+1 ?
A PIECE OF CAKE BRAINTEASER! π
On his birthday next year, in 2024, Nathan will be N years old. He looks forward to then having a cake with N candles on it. Imagine making triangles by connecting every possible distinct trio of three candles on the cake. Then there would be precisely 364 different triangles, to match the days in 2024 ! π
The brainteaser is to figure out the value of N.
JOKE π
What did the Chinese philosopher Li Ping say about the other two days…?
“Did you miss today’s joke?”
but I thought she said, “Did you miss two days…joke?!!” π
AS EASY AS ABC…! π
Which three-digit positive whole number ABC is exactly equal to AA + BB + CC? Can you prove that the solution is unique?
A THREE-PEOPLE PUZZLE FROM 11 YEARS AGO πππ
A good family photo of Jenny, Michael & myself πππ
I am six years older than Jenny, and she is thirty years older than Michael. How old will Michael be when (in future, God-willing) the total of our three ages will be as close as possible to 154?
NUMBER WORD PUZZLE π
The number-word ONE HUNDRED AND FIFTY-FOUR contains all the five official English alphabet vowels, A, E, I, O, U. What is the smallest positive whole number for which its number-word contains all the vowels A, E, I, O, U exactly once each? (Hint: The correct number is greater than 154.)
FAST EASTER WORD PUZZLE π
Rearrange the letters of EASTER to make a different, proper six-letter English word that does not begin with E.
AN ELEGANT CHESS PUZZLE β
Black has an invisible pawn somewhere on the b-file. Where on the b-file is the pawn not located if it’s White to play and force checkmate in 4 moves? π
It’s my intention to publish solutions to all the puzzles around the time that blog post #155 comes out, God-willing as always.
In the meantime, please do feel free to send me your best solutions to any or all of the puzzles, if you like π.
I would like to round off this article now by most sincerely wishing you a very blessed month of April, with lots of happiness in everything that you do β€.
With kindest wishes as always,
Paul Mπtwani β€
“For God so loved the world that He gave His one and only Son, that whoever believes in Him shall not perish but have eternal life.”–John 3:16.
P.S. = Puzzle Solutions (being posted on 19.4.2023)
In the cuboid brainteaser, 2(LW+LH+WH)=386βLW+LH+WH=193. So, 193+H2 = LW+LH+WH+H2 = L(W+H)+H(W+H) = (L+H)(W+H), a neat and noteworthy algebraic trick πβ
Now trying H=1: 194 = (L+1)(W+1)β2 x 97 = (L+1)(W+1), but then L = 1 and W = 96 (or vice-versa), and that’s not OK because H & L should be different (like the siblings’ ages), and also none of them should be 96 in this puzzle!!
Trying H=2: 197 is a prime number; it can’t equal (L+2)(W+2), since L & W have to be positive. (We can’t allow L+2=1 & W+2=197, for example, because we’d get L=-1.)
Trying H=3: 202 = 2 x 101, which can’t equal (L+3)(W+3) in any suitable way.
Trying H=4: 209 = 11 x 19 = (L+4)(W+4) with L=7 & W=15, for example.
So, a solution for the siblings’ ages is 4, 7 and 15, with the ‘main’ girl in the puzzle being 15 (the oldest one).
If we were to investigate further, we wouldn’t find any truly different solutions, though of course H=7 or H=15 are possible, and would lead to L & W being 4 & 15 or 4 & 7. We still end up with the same set of dimensions (and siblings’ ages): 4, 7 & definitely 15 for the girl π
The ‘2023’ puzzle can be solved nicely like this: since 2016 is a multiple of 9 (224 x 9=2016) and 2023 = 7 + 2016, then the number S = 7999…999 (starting with a 7 followed by 224 nines) will be the smallest number–using the least-possible number of digits–whose digits sum equals 2023. Therefore, S+1 = 8000…000 (starting with an 8 followed by 224 zeroes), and so its digits sum is simply 8. π
When there are N candles on Nathan’s cake, the number of different trios of candles that we could connect to get triangles is N x (N-1) x (N-2) Γ· 6. (We divide by 6, because we don’t want to miscount any same trio 6 times just because that same trio could be listed in 6 different orders.) We were basically given that N x (N-1) x (N-2) Γ· 6 = 364, and so N x (N-1) x (N-2) = 2184. We observe that N-1 should be pretty close to the cube root of 2184, which is 12.974…, very close to 13. That suggests N = 14, and indeed 14 x 13 x 12 = 2184. So, it’s confirmed: N = 14. π
In the ‘ABC’ puzzle, ABC = 198, the unique solution π
Proof: Given ABC = AA + BB + CC in this particular puzzle, then consideration of the true ‘place values’ of the digits leads toβ100A + 10B + C = 10A + A + 10B + B + 10C + C, which rearranges toβ89A = B + 10C. Since 10C + B can’t be big enough to be a three-digit number (because C & B are numbers not bigger than 9), it follows that 89A has to just be a two-digit number, and therefore A = 1. Then 10C + B = 89, which forces C = 8 & B = 9. It’s confirmed: ABC = 198. π That lovely, special number always reminds me of 1998, the year when my son, Michael, was born π
In my family puzzle, when Michael is 29 (God-willing), Jenny 59 & Paul 65, the total of the three ages will be 153, which is the closest it can get to 154 before shooting past there! π
TWO HUNDRED AND SIX contains vowels A, E, I, O & U exactly once each. π
EASTERβTEASER π
In the Chess puzzle…
White forces checkmate quickly, with the ‘main’ line being 1 Qg8+ Kd6 2 Qd8+ Ke6 3 Qc8+ Kd6 4 Bc5#, provided that Black’s invisible b-pawn is not on b6 !! ππ€£
