Dear Friends,
In the past fifty years since I was first introduced to the Royal Game of Chess at the age of 11 in Scotland, I can truly say with gratitude that I have met thousands of lovely people through the beautiful game. I still remember many of the moves that were played, but I remember the people much more!
Even if one can’t always personally let everyone know that they are very fondly thought of and remembered, there’s no better time than the present to let people know we care. 💕

Jenny (whom I married soon after) is pictured with Harald Fietz,
Ian Grant and Jonathan Grant, whose birthday is coming up in just a few days from now 😊.

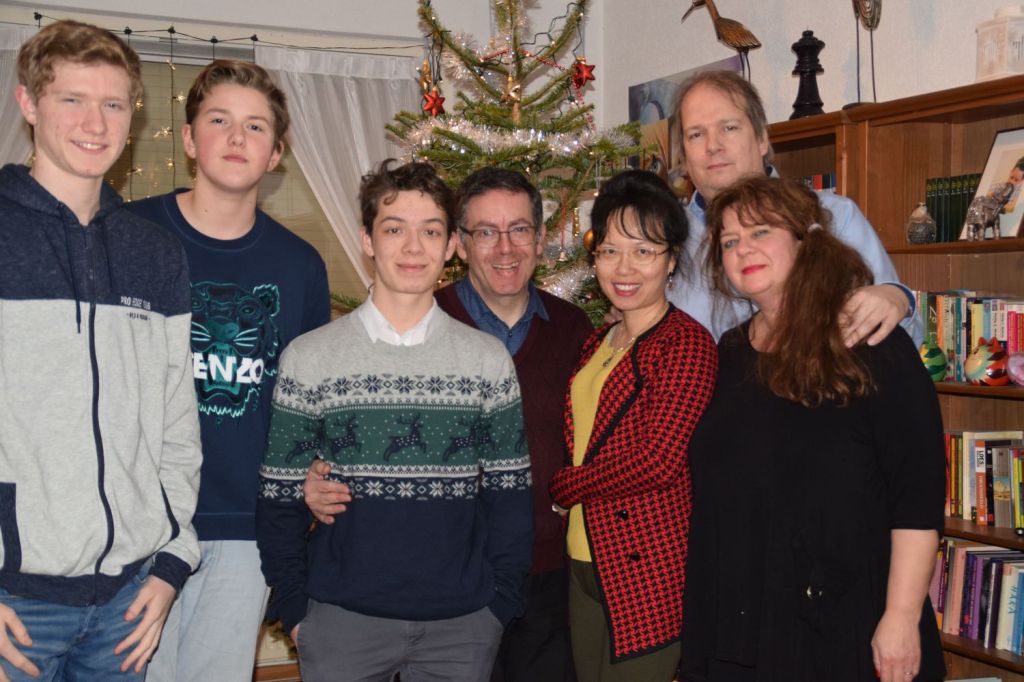
in early June, exactly Ax3 days from today…😁
Early Birthday Puzzle in Honour of Chess Friends Jonathan Grant, Andrée Upton-Regnier & Erika Sziva ❤️
Today (May 18) is day number 139 of this year 2024. So, Jonathan’s birthday coming up will be on day number J of this year, where J is clearly greater than 139. Andrée’s birthday will be A days after Jonathan’s, where J x A = 1001. Also, Erika’s birthday will be A x 3 days from today.
Your fun puzzle is to figure out the exact dates (month & day number) of the birthdays of Jonathan, Andrée and Erika. 👍👌🙌
Some of my dear friends have passed on, but they will never be forgotten either ❤️

Shaun, Mike P., Andrew, Gary, Tony, Mike H., Mike D. and Martin.
Martin Jackson and Tony Welsh have passed on, but will always be remembered fondly ❤️

with dear friends Tim Upton (19.12.1958-10.1.2018) and Graham Morrison (10.11.1958-13.5.2024).
Graham was Scottish Champion in 1981, and represented Scotland frequently
at international level, playing in Olympiads in 1984, 1988, 2010 & 2012,
and in many European Team Championships.
He was also a long-standing player in the 4NCL, formerly with Barbican before moving to Alba.
I had been very much looking forward to seeing Graham at the British Chess Championships
this summer, as he had also signed up to take part.
He was a really lovely, kind and gentle man ❤️
who will be missed greatly by all who knew him well.
Sincere condolences and thoughts go to Graham’s wife, Lynne.

is based on a game of Graham’s from the 1989 Edinburgh Open, 35 years ago!
Graham loved to have the bishop pair in Chess, and he frequently used it to great effect.
Enjoy finding the strongest directly-winning idea, just like FIDE Master Graham Morrison did! 😍
I was invited recently to do a ‘simultaneous exhibition’, playing more than 20 Chess members and friends of Boey-Temse Chess Club, celebrating the thriving club’s first 50 years (1974-2024). I would like to specially thank Marc Blommaert (Club Chairman/President) for the wonderful invitation; Luc De Ryck (former long-time Mayor of Temse) for his delightful speech; Wim Van Rossen (Alderman and prominent board member of ‘Gemeente Temse’) for his very thoughtful words and generous gift too ❤️.

Many of the photos are published with the kind permission of professional photographer Julien Heerwegh, while others were sent to me by Rita Ysewyn, Geert Vanstraelen, Geert Wille, Bart Vereecken, Marc De Meireleir and Marc Blommaert. (I have saved some photos for future occasions 😊.)

In the Chess games with Willem Verrijdt, Wiebke Barbier, Rudy Van Laeken, Kurt De Maeyer, Luc De Ryck, Robin Blommaert, Jonas De Bock, Emiel Slachmuylders, Loic Verbeke, Bjorn Dijckmans, Gust Van Der Meiren, Hugo Stuer, Geert Wille, Marc Blommaert, Marcel Wynants, Steven Lippens, Geert Vanstraelen, Luc Vereecken, Wim Van Rossen, Wim Barbier and Pascal Kegels, everyone fought well, and Pascal got a draw…and very nearly more! It was a great pleasure for me to give prizes for everyone. (Felix Verelst was also going to play, but hopefully we’ll meet at a future celebration.)








I enjoy great movies as much as Chess! One of my absolute favourite pieces of film music was John Barry’s “Dawn Raid on Fort Knox” from 60 years ago in the 1964 James Bond “Goldfinger” 👌❤️
https://www.youtube.com/watch?v=nnW-8YpQpgQ (5 minutes 48 seconds).
I was reminded of it by a game in the ‘simul’ which reached the following position from the Fort Knox variation of the French Defence…
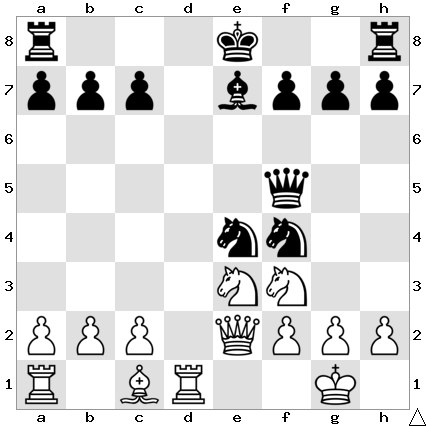
One of the brilliant mathematicians who played against me in the ‘simul’ was Robin Blommaert, son of Marc Blommaert. Their birthdays are both in July, but I’ll be seeing them sooner, this month. For their enjoyment–and hopefully yours too!!–I decided to compose a couple of nice puzzles in which I’m also thinking of Harriet, a dear colleague whose birthday was/is this month, and my wife Jenny who’s turning 56 next month.
Fun Puzzle in Honour of Harriet and Jenny! 💕
I saw a great film one day in April. The ‘Film day’ number F was of course something between 1 and 30 inclusive. The day number H of Harriet’s birthday in May was/is of course something between 1 and 31 inclusive. If I add up F and H and also the number of days from the Film day until Harriet’s birthday, the result is 56.
Your fun puzzle is now to figure out the exact day number in May of Harriet’s birthday! 😍
B😊nus Fun Puzzle in Honour of my youngest sister & her husband (my brother-in-law) 😊❤️
My youngest sister and her husband recently celebrated their Silver Wedding Anniversary and their birthdays too.
For simplicity in this puzzle, let’s suppose that their birthdays are on the same day as each other (same month and day number).
We’ll say that S is my sister’s age and B is my brother-in-law’s age.
Imagine calculating their sum, their difference, and their product too. Then calculate the total sum T of all of that!
I will tell you honestly that, in their case, T is always a square number, every year.
Your fun puzzle is now to figure out the age difference (in years) of my sister and her husband. 🙌💕
Word Puzzle
Rearrange the letters of LEGACY IN SUN to make a proper 11-letter English word which describes how God loves us all.
I’ve in general been so busy for quite a long time that I must soon catch up a bit with publishing solutions to various puzzles in certain previous articles, but in the meantime I wish you oodles of enjoyment with all the puzzles 😁, and please do feel free to send me your solutions by email, if you like. 👍
With kindest wishes as always,
Paul M😊twani ❤️
I’ll conclude this Blog Post #167 with the beautiful Bible Psalm 67:1