Dear Readers,
Let’s begin with a quick, wee warm-up of three checkmate puzzles in 3, 3 or 3+3 moves based on a trio of actual games from…1925 ! 😁
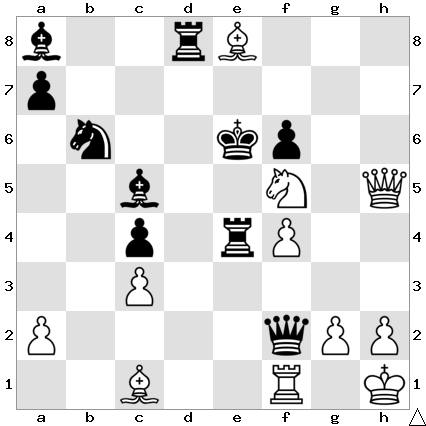


Checkmate Puzzle Solutions
A) 1 Qf7+! Kxf5 2 g4+ Kxg4 3 Qh5#
B) 1 Rxe6! leaves Black with nothing better than 1…Rff7 2 Bxg7+! Rxg7 3 Re8#
C) 1 Rxh7+! Kxh7 2 Qh3+ Kg6 3 Qh6+ Kf5 4 Qh7+! Kg4 5 Qh3# or 4…Rg6 5 Qh3+ Ke4 6 Nc3#

The multiple purposes of this article include:- most sincerely wishing everyone a very blessed, happy New Year; writing about a wonderfully-organised international Chess festival which concluded on December 30 in Groningen in the North of The Netherlands; sharing some good fun freshly-created puzzles (involving Chess, Mathematics and more); sharing a vitally-important reflection which I honestly know more about, with certainty, than anything else I know. Indeed, it’s the duty of everyone who knows the Good News to share it with others, in the hope that they will come to love, respect and accept with gratitude to God the priceless gift which He offers freely to everyone. Peoples’ individual decisions to accept the gift (or not) will be of eternal importance, so it’s not something to ignore or delay.



❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️

Since the age of 11, I have enjoyed taking part in nice Chess events during some of my ‘free’ time. Currently, I play competitive Chess only during school holidays, because throughout term times I dedicate a lot of time and energy to giving the highest quality of Mathematics teaching that I can for all of my students. Also, time with family and time to rest well is always important.
I am grateful to Mr. Govert Pellikaan and his fantastic team of organisers & arbiters who made the splendid Groningen Chess Festival run really smoothly for the enjoyment of around 400 people who took part. Meeting so many friendly people was a great pleasure.


Many participants chose for one of the 9-round Open sections, while some others opted for a 4-player, 3-round, all-play-all mini-group. Yet others (including myself) were more than happy with the possibility of playing in a compact 5-round event starting on Boxing Day (26 December). Whichever event one chooses for, it’s highly appealing that its schedule requires just one game per day.
Everyone plays together in a lovely, spacious hall. Drinks, snacks and meals are readily available within the analysis room of the same building, at good prices.
A superb Chess bookstall is provided by Robert Klomp and his wife, WGM Erika Sziva, whose website is http://www.debestezet.nl 👍❤️ The thriving business was founded in 1994.

I was delighted to win the Senior Tournament with 5/5, and the next day my wife (Jenny) and I celebrated New Year’s Eve at the home of Robert & Erika in the Dutch town of Best, where we stayed until the evening of New Year’s Day—a favourite, long-standing tradition with our families 😊😊





Orange is a national colour in The Netherlands.

Jenny and I have gone a long way to reach number 63, with some special thoughts in mind…
for bringing you six threes with a sneaky, fun twist!
Think of the year 1925, from a century ago. Reverse its digits to get 5291.
Multiply by 63, and the result is a super six-digit string 333333
consisting entirely of 3s; my absolute favourite! 😁
Question: How can you use the numbers 100, 64, 3 and my house-number 11 to get 21.12, to remind you of December 21, the date when the annual Groningen Chess Festival begins?

Answer: 64 x 3 x 11 ÷ 100 = 21.12 👍😁
Word Puzzle: Can you read my mind and rearrange the 18 letters of CONGRESS BEGINS THEN to make 3 other very particular words!?

Answer: I was thinking of
CONGRESS BEGINS THEN =
BEST GRONINGEN CHESS 👍😊❤️
Nice Number Puzzle: Why is today, 3.1.25, a nice day for me to gratefully celebrate a 5/5 result?

who was the runner-up on 4/5 in the Senior Tournament.
Answer: 5 to the power of 5 equals 3125 🙌😁

and GM Thomas Beersden were 6 of the top 7 prizewinners in the Open A-Group.
IM Nick Maatman would also have been pictured, but he had had to leave, sick.
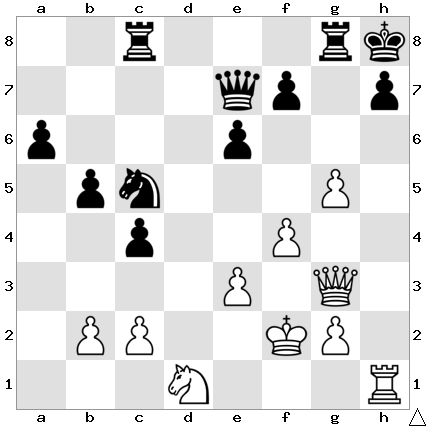
Given that 17-year-old Machteld Van Foreest is a local player from Groningen, her IM norm achievement was a particularly popular result. Today, I have been enjoying playing through some of Machteld’s earlier victories from 2024. I have chosen the following position from the Dutch League, in which it was Machteld as White to play and win by force…and she did so! 😁


The game ended crisply with 1 Re6! Qg5 2 f4! 1-0. Black resigned in view of 2…Qh4 3 Rh6#. It’s true that 1…Qh7 would have been more tenacious, but White would still have won comfortably with 2 Qf4!, intending 2…Rxd5 3 Rh6.
Literally hundreds of great photos were taken by Bart Beijer and Harry Gielen at the tournament. Though I can’t feature all of them here, I do want to congratulate most sincerely every person who was there in Groningen, for everyone’s presence contributed to making an unforgettable event 💕
It was especially nice for me to see Mr. Johan Zwanepol, who was the main organiser when I previously played in Groningen in 1979, 1980, 1989 and 1990 😊


He still deserves ’10/10′ for excellent, courageous play.
Rishi loves Maths, too. So, here comes a nice puzzle in his honour…
Without needing to use a calculator or any other external aids, can you figure out mentally the exact value of the square root of (1+3+5+…+2023+2025)?

The key secret is that the total sum of 1+3+5+…+the nth odd number
always equals n squared exactly. Since 2025 = 2 x 1013 – 1, we can know that 2025 is the 1013th odd number. So, 1+3+5+…+2023+2025 must equal exactly 1013 squared. Taking the square root leaves us with 1013 in honour of 13-year-old Rishi (to whom I awarded 10 points) 🙌😊
Chess Helpmate Puzzle

It’s Black to play and co-operate fully in a Helpmate in six moves! That is, Black starts a co-operative sequence which ends with White delivering checkmate on his 6th move. Can you do as well as Problem-Solving Chess Grandmaster Dolf Wissmann by cracking the puzzle in under a minute!? 👌

Solution:

1…g5 2 Kf2 g4 3 Ke3 g3 4 Kd4 g2 5 Kxd5 g1=B 6 Kc6 Ba7 7 Kc7#
Bonus Two-Part Fantasy Chess Puzzle 💕
- What is the maximum number of rooks which can be placed on an empty Chess board such that none of them are attacking each other?
- What is the maximum number of knights which can be placed on an empty Chess board such that none of them are attacking each other?

Answers
- Eight rooks, placed on a common long diagonal of a Chess board, will not be attacking each other.
- 32 knights, either all on dark squares or all on light squares, will not be attacking each other.

A Happy New Year Trigonometry Puzzle In Honour of
Chief Arbiter Erwin Denissen, who is also a Mathematics Teacher

Without needing to use a calculator or any other external aids, figure out mentally the exact value of the square root of sin 2025° * cos 2025° * tan 2025°

Answer:
sin x° * cos x° * tan x° = sin x° * cos x° * (sin x° ÷ cos x°) = (sin x°) squared, and so its square root will be the absolute value of sin x°.
sin 2025° = sin (5 x 360 + 225)° = sin 225° = -sin 45° = -1/sqrt 2.
Its absolute value is 1/sqrt 2 or equivalently (sqrt 2) ÷ 2.
Another Sneaky Square Root Surprise!
Think about the square root of 2025. What surprise do we get if we increase each digit of 2025 by 1 and then take the square root?

Answer: The square root of 2025 is 45. The square root of 3136 is 56. Both digits in the answer increased by 1, too! 😁
I will round off this article with one final nice photo and a beautiful, true quotation.
