Month: June 2023

Dear All,

The birthdays coming on weekdays next week include my birthday in n days from now and my wife’s birthday in 3n/2 days’ time 💖. In the meantime, though, Jenny and I would like to wish both a very happy birthday tomorrow to our dear friend WGM (Woman Chess Grandmaster) Erika Sziva, and a continued strong recovery from her recent operation in hospital.

We would also like to wish a really happy birthday later on in 2n = 2*n days from now to Richard, one of the lovely new friends whom we met recently at a super party in Luxembourg 😊🎂💖

Puzzle #1

As 3 is my absolute favourite number, this first fun warm-up puzzle is a triple or three-part puzzle 😊😊😊…It’s to figure out the dates this month of Jenny’s birthday, Richard’s birthday, and the number of prizes that were in my bag 🌹

Puzzle #2: Double Brainteaser for Jerry & all Maths fans! 😎

A rectangle (that is not a square) has a perimeter of P units (e.g. P cm) and an area of A square units (e.g. A cm²).

Part 1: It can be proved that, for all such rectangles, P² > J*A, where J is a particular, special whole number. Enjoy figuring out, with proof, the maximum value for J that still makes the inequality P² > J*A true for all such rectangles.

Part 2 of the brainteaser is to figure out (with proof) an expression in terms of P and A for the radius of the largest circle which can fit inside the rectangle. 👏

🎶 There is a noteworthy spiritual analogy…God makes His Holy Spirit available to guide and help us at all times. When we stay ‘tuned in’ and properly connected within, all is well. In our lives now, we should remember and respect where the boundaries are.

Puzzle #3: Rectangles & Squares Double Brainteaser 😃

The diagram shows a large square (with a dark-coloured outline) containing four congruent rectangles and another square, which all fit in exactly.

Part 1: If the area of the large square is A square units, find (with proof) an expression in terms of A for the perimeter of one of the inner rectangles.

Part 2: Suppose that the perimeter of the inner square is not less than the perimeter of one of the four congruent rectangles. Determine (with proof) the minimum possible value of the ratio longer side : shorter side for any of the four congruent rectangles. ✔

Puzzle #4: A Power of Love Brainteaser 💖^💖

Since God is perfect Love, Love really ought to have 1st place in our lives. So, L=1 in this brainteaser. I discovered that if LOVE is a four-digit whole number–and therefore OV is a two-digit whole number–then there is just one, unique solution to the equation

LOVE = OV * E^E (with L=1).

Your lovely brainteaser is to figure out (with proof) the value of the number represented here by LOVE. 💖

Puzzle #5: A Loving Sequel Starring Coco the Cute Cat!! 🐱‍👓

When solving Puzzle #4, Cute Coco, a super-mathematical cat, found the correct value for LOVE.

Now in Puzzle #5, and here in Blog Post #158, it’s fitting that

158 * C + D = LOVE,

where D is the day-number in June of my birthday, and C is a nice, positive number in honour of clever Coco 🐱‍🚀

Your fun puzzle is to figure out the values of C and D. 👍👍

P.S. I hope you’ll enjoy all the puzzles every bit as much as Coco’s owner, Mr. Jan Vanderwegen, who is Musica Mundi School’s excellent I.T. Manager 👍😊

Puzzle #6: A Word Puzzle in Honour of Coco 💕

Can you think of a plural, 11-letter, proper English word starting with the letters coco which refers to two (or more) people who create something together? 🎶

Puzzle #7: Black to play & force checkmate in 8 moves 😍

For all chess-related items, I can warmly recommend http://www.debestezet.nl, a top-quality site 👍 run by WGM Erika Sziva and her husband, Robert Klomp. Erika & Robert also have http://www.raindroptime.com 💕

It’s my intention to publish solutions to all the puzzles around the time that blog post #159 comes out, God-willing as always.

In the meantime, please do feel free to send me your best solutions to any or all of the puzzles, if you like 😊.

I would like to round off this article by most sincerely wishing you a very blessed month of June, with lots of happiness in everything that you do ❤.

Also, I would like to particularly wish all students of Musica Mundi School success in their class concerts next week, and in all the other exciting events still to come in the remainder of the current school year 🎶😍. For the graduating students, I am sure that their research presentations and musical performances will be wonderful and extremely interesting 👏. One of the students who is about to graduate is Antigone, and it’s also her birthday this week. Happy birthday, and have a really wonderful time, Antigone! 🎂😊

With kindest wishes as always,

Paul M😊twani ❤

“My Father is glorified and honored by this, when you bear much fruit, and prove yourselves to be My true disciples.”–Bible verse, John 15:8 💕

P.S. = Puzzle Solutions (being posted–at last!–now on Tuesday 29 August 2023)

Puzzle #1: n=6; Jenny’s birthday was 16 June; Richard’s birthday was 19 June; there were 6+2=8 prizes in my bag 😊

Puzzle #2: Part 1

If the rectangle’s Length, Width & Area are represented by L, W & A respectively, then

L*W=A

so W = A/L.

Also, the Perimeter, P=2L+2W

→P=2L+2(A/L)

→2L²-PL+2A=0, which can be thought of as a Quadratic Equation in L.

The standard textbook condition for it to have two distinct, real solutions for L (corresponding to the cases L ˃ W or, alternatively, L < W)

is that its Discriminant b²-4ac ˃ 0.

In this case, that means (-P)²-4*2*2A ˃ 0

which simplifies to give P² ˃ 16A.

The puzzle stated that P² ˃ J*A.

So, now we have discovered that J = 16, the maximum value for J that would be guaranteed to hold true for every rectangle that is not square. Note that, specifically for all squares, P² = 16A exactly, and so it’s actually pretty logical then that P² ˃ 16A for non-square rectangles. 😎

Puzzle #2: Part 2

Now imagine fitting a circle of radius r inside the rectangle.

Let’s assume that L < W (though the correct final expression for r_max will not change at all even if L ˃ W).

The diameter of our circle cannot exceed L, as otherwise some of the circle would be outside the rectangle.

So, the maximum value of r is such that 2r = L → r_max = L/2.

Returning now to our earlier Quadratic Equation 2L²-PL+2A=0,

and using the standard Quadratic Formula given in lots of textbooks,

the smaller of the two solutions for L (corresponding to L < W ) is given by

L = (P – sqrt(P² – 16A))/4.

Therefore, since we already deduced that r_max = L/2,

we now reach the result that r_max = (P – sqrt(P² – 16A))/8. 😍

Puzzle #3:

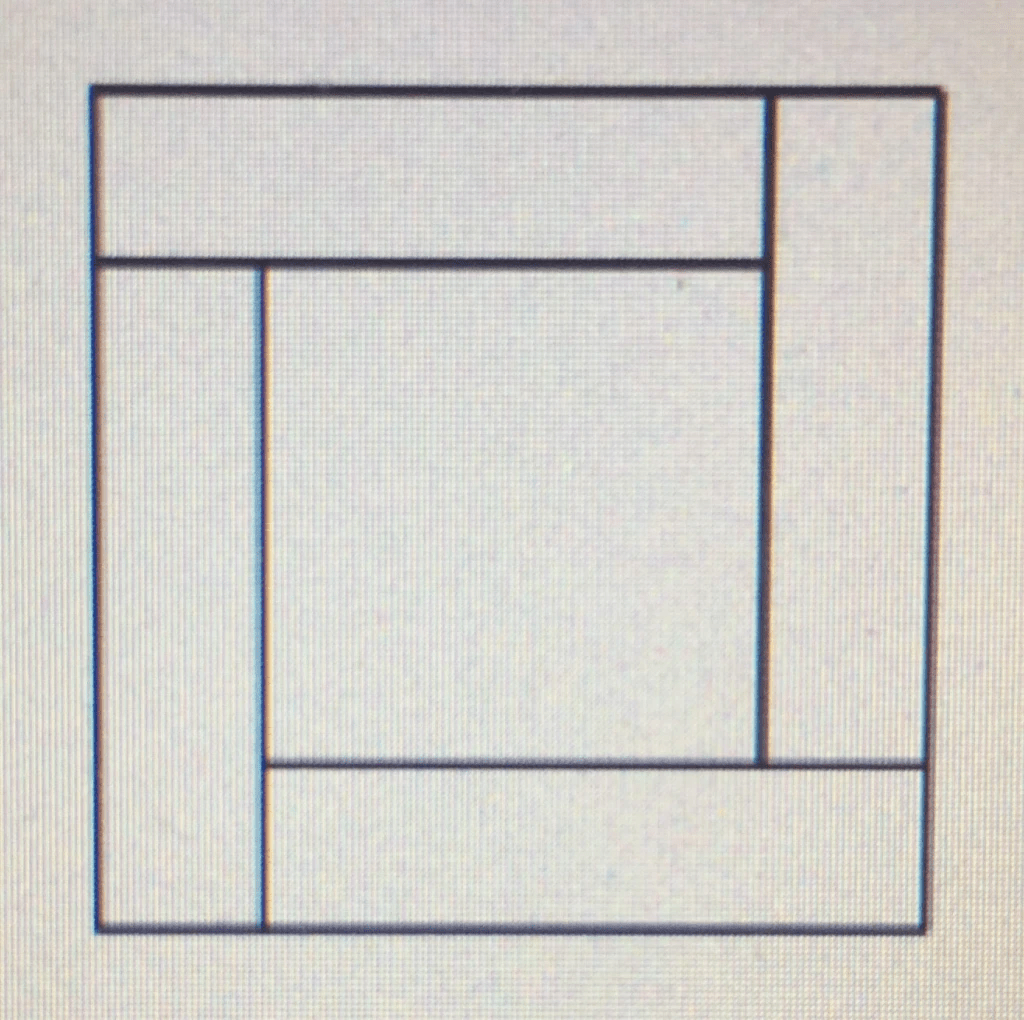
Part 1

Let the four congruent inner rectangles each have dimensions L & W.

They then each have a perimeter of P = 2*(L+W).

Also, each side of the large square is L+W, and its area is therefore given by

A = (L+W)²

→L+W = sqrt(A)

and so

P = 2*sqrt(A). 👌

Part 2

Let’s assume that L < W.

Then note that each side of the inner square will be W – L.

If its perimeter is not less than the perimeter of one of the aforementioned rectangles, then

4*(W-L)≥2*(L+W)

→4W-4L ≥ 2L+2W

→2W ≥ 6L

and so

W/L ≥ 3. 👍 (If we had assumed W < L, we would have ended up with L/W ≥ 3.)

Puzzle #4

The unique solution to LOVE = OV * E^E (with L=1) is OV=59 & E=3, so LOVE=1593=59*3³ 💖

Restrictions on the size of OV * E^E (big enough to get a four-digit result, yet not too large given that L = 1 only) helped to narrow down the options and home in quickly on the one correct solution 😊✔

Puzzle #5

Given 158 * C + D = LOVE = 1593 now,

it’s clear that C = 10 & D = 13 works perfectly 💕

Puzzle #6

COCOMPOSERS ! 😁😁🎶🎶

Puzzle #7

The main checkmating sequence is 1…Qe2+ 2 Kg2 Nh4+ 3 Kg3 (or 3 Kg1 Qe1+ 4 Rxe1 Rxe1#) 3…Re3+!, after which White’s line of best resistance is 4 fxe3 Nf5+ 5 Kf4 Qxe3+ 6 Kxg4 (6 Kxf5 Qg5#) 6…Nh6+ 7 Kh4 Qg5+ 8 Kh3 Qg4# 👏♟

Special congratulations to the Van Steerteghem Family of Eric, Martine, Nick and (last, but certainly not least!!) my brilliant colleague, Jens. They tackle and solve the puzzles with great enthusiasm and success! 👍😊

In a future blog post, I will enjoy sharing with you some of the nice puzzles that they gave me for my birthday.

For now, though, I will simply conclude this post here with three lovely photos of my top puzzle solvers! 😁😁😁